Research Work

• 研究紹介
• 研究業績

研究紹介

表面張力を利用した物質運動の数理解析

関連する研究費

• 科学研究費補助金 若手研究（Ｂ），2002年度〜2003年度
• 科学研究費補助金 若手研究（Ａ），2006年度〜2008年度
• 科学研究費補助金 基盤研究（Ｂ），2009年度〜2012年度

化学反応を伴う粒子運動の数理解析

液滴運動の数理モデルとその数理解析

液滴運動を表現する数理モデルは，液滴の高さを表現する変数を導入することによって，液滴の表面，水面を1つの関数を用いて表し，その関数を用いて表面エネルギー最小化から導出することに成功した．この方程式は特異性を持つ双曲型偏微分方程式となった．また，液滴から展開される界面活性膜を反応拡散系で近似することによって水面の表面張力変化を表現することにした．これと液滴の体積保存条件を加えることによって液滴運動を記述する数理モデルを構成した．この数理モデル中の液滴モデルが特異性を持つことと初期体積保存の制約条件を持つことから一般の差分による数値計算が困難であった．そこで離散勾配流を用いて数値計算をおこなった．その結果，１）小さな液滴は自走する，２）大きな液滴は分裂し自走する，３）分裂した液滴は衝突角度に依存して反射する場合と融合する場合がある，等の結果を得た．

液滴の融合現象

液滴の反射現象

ロウソク火炎振動子の同期現象に対する数理モデルとその数理解析
（科学研究費補助金 萌芽研究，2007年度〜2009年度）

ロウソク火炎振動モデルの構成

複数の洋ロウソクを束ねて火をつけると炎が振動する現象がある． この炎が振動するロウソクの束をロウソク振動子と呼ぶことにする． ロウソク振動子を2つ用意して，適当に置くとロウソク振動子間の距離に 依存して炎の同期現象が報告された． この引き込み現象を起こす機構を数理的に理解することが研究の目的である．

1本のロウソクに火を点けると炎は一定形状を保ちながら燃焼し続けます．ところが，複数本束ねたロウソクに火を点けると炎の形状は一定周波数で振動しながら燃焼し続けるようになります．このロウソク火炎が振動する機構は，(ロウソクの本数が増えることで)ロウの供給と酸素の供給のバランスが崩れることによって生じる完全燃焼と不完全燃焼を繰り返すためだと考えられています．この振動している一組のロウソク火炎をロウソク振動子と呼ぶことにします．さて，このロウソク振動子を2組用意し並べて設置すると，その距離に応じて異なる同期現象が起こります．その距離が十分に近いと同位相同期し(図1(a))，適当に離れていると逆位相同期する(図1(b))ようになるのです．この同期現象はどのようにして起こっているのでしょうか？一見，2組のロウソクの酸素の奪い合いのように思えますが・・

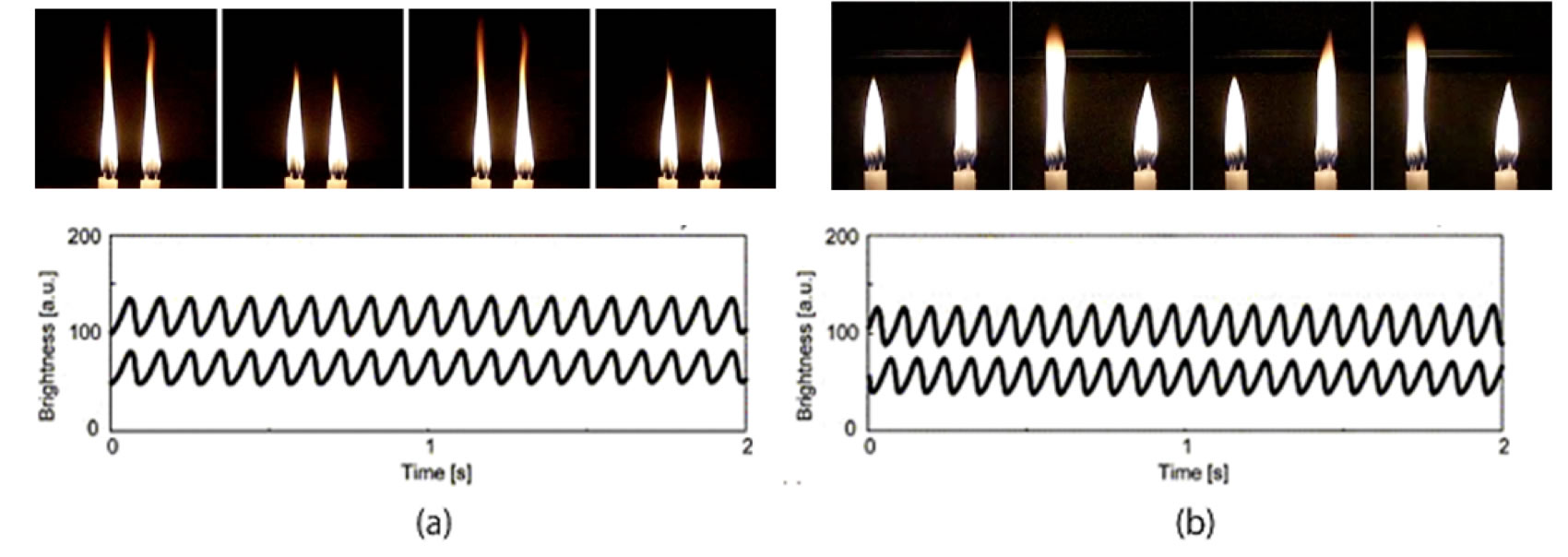
　　　　　　　　　　　　　　　　　　　　図１

工事中

 

生理学と協働した数理科学による皮膚疾患機構の解明
（ＪＳＴ CREST研究課題，2010年度〜2015年度）

トップに戻る

Research Papers

　
• [25] M.Yadome,K-I.Ueda and M.Nagayama, "Chaotic motion of propagating pulses in the Gray-Scott model", Physical Review E, 83(2011) 056207.
• [24] M.Nagayama,K-I.Ueda and M.Yadome, "Numerical approach for transient dynamics of oscillatory pulses in a bistable reaction-diffusion system", Japan Journal of Industrial and Applied Mathmatics, 27(2) (2010) 295--322.
• [23] N.J.Suematsu, Y.Ikura, M.Nagayama, N.Kawagishi, M.Nakamura, H.Kitahata, M.Murakami and S.Nakata, "Mode-switching of the self-motion of a camphor boat depending on the diffusion distance of camphor molecules", Journal of Physical Chemistry, 114(2010) 9876-9882.
• [22] K.Iida, N.J.Suematsu, Y.Miyahara, H.Kitahata, M.Nagayama and S.Nakata, "Experimental and theoretical studies on the self-motion of a phenanthroline disk coupled with complex formation", Physical Chemistry Chemical Physics, 12(2010) 1557-1563.
• [21] M.Tsutsumi, H.Kitahata, S.Nakata, Y.Sanno, M.Nagayama and M.Denda, " Mathematical analysis of intercellular calcium propagation induced by adenosine triphosphate", Skin Research and Technology, 16(2010) 146-150.
• [20] H.Kitahata, J.Taguchi, M.Nagayama, T.Sakurai, Y.Ikura, A.Osa, Y.Sumino, M.Tanaka, E.Yokoyama and H.Miike, "Oscillation and synchronization in combustion of candles: Radiation coupling could induce synchronization of oscillatory combustion", Journal of Physical Chemistry (A), 113(29) (2009) 8164-8168.
• [19] M.Nagayama, M.Yadome, N.Kato, J.Kirisaka, M.Murakami and S.Nakata, "Bifurcation of self-motion depending on the reaction order",  Physical Chemistry Chemical Physics, 11(2009) 1085-1090.
• [18] M.Yadome, K.-I.Ueda, T.Teramoto, M.Nagayama and Y.Nishiura, "Periodic transition sequences of scattering patterns in a three-component reaction-diffusion system", Bulletin of the Institute of Mathematics, Academia Sinica New Series, 3(4)(2008) 585-602.
• [17] S.-I.Ei, M.Mimura and M.Nagayama, "Interacting spots in reaction diffusion systems ",  Discrete and Continuous Dynamical Systems, 14(1)(2006) 31-62.
• [16] Y.Sumino, M.Nagayama, H.Kitahata, S.M.Nomura, N.Magome, Y.Mori and K.Yoshikkawa, "Chemo-Sensitive Running Droplet ",   Physical Review E 72(2005) 041603.
• [15] T.Ikeda, M.Nagayama and H.Ikeda,"Bifurcation of helical wave from travelling wave ",  Jpn. J. Indast. Appl. Math. 21(3)(2004) 405-424.
• [14] M.Nagayama, S.Nakata, Y.Doi and Y.Hayashima, " A theoretical and experimental study on the unidirectional motion of a camphor disk ", Physica D, 194(2004) 151-165.
• [13] M.Mimura, M.Nagayama and T.Ohta, "Non-annihilation of travelling pulses in reaction-diffusion systems, ", Methods and Applications of Analysis, 9(4)(2002) 493-516.
• [12] S.-I.Ei, M.Mimura and M.Nagayama, "Pulse-pulse interaction in Reaction-Diffusion system ", Physica D, 165(2002) 176-198.
• [11] Y.Hayashima, M.Nagayama, Y.Doi, S.Nakata, M.Kimura and M.Iida, "Self-motion of a camphoric acid boat sensitive to chemical environment ", Phys.Chem.Chem.Phys.,4(2002) 1386-1392.
• [10] M.Nagayama, H.Okamoto and J.Zhu, "On the blow-up of some similarity solutions of the Navier-Stokes equations ", Quaderni di Matematica 10 (2002) 139-162.
• [9] M.Nagayama and H.Okamoto," On the interior layer appearing in the similarity solutions of the Navier-Stokes equations ", Jpn. J. Indast. Appl.Math. 19(2) (2002) 277-300.
• [8] M.Nagayama, T.Ikeda, T.Ishiwata, N.Tamura and M.Ohyanagi, "Three-dimensional numerical simulation of helically propagating combustion waves ", Journal of Materials Synthesis and Processing 9(3) (2001) 153-163.
• [7] M.I.Kohira, Y.Hayashima, M.Nagayama and S.Nakata,"Synchronized self-motion of two camphor boats ", Langmuir 17 (2001) 7124-7129.
• [6] T.Ikeda and M.Nagayama,"Helical Combustion Waves in Self-propagating High-temperature Syntheses ", Bulletin of the Japan Society for Industrial and Applied Mathematics 11(2) (2001) 40-48 (in Japanese).
• [5] Y.Hayashima, M.Nagayama and S.Nakata,"A camphor oscillates while breaking symmetry ",Journal of Physical Chemistry B 105(22) (2001) 5353-5357.
• [4] M.Mimura, M.Nagayama, H.Ikeda and T.Ikeda, "Dynamics of travelling breathers arising in reaction-diffusion systems -- ODE modelling approach -- ", Hiroshima Math. J. 30(2) (2000) 221-256.
• [3] M.Mimura, M.Nagayama and K.Sakamoto, "Singular Hopf-bifurcation in a chemical reaction-diffusion system", Appl. Math. Lett. 11(4) (1998) 127-131.
• [2] M.Mimura and M.Nagayama, "Nonannihilation dynamics in an exothermic reaction-diffusion system with mono-stable excitability", CHAOS 7(4) (1997) 817-826.
• [1] M.Mimura, M.Nagayama and K.Sakamoto, "Pattern dynamics in an exothermic reaction", Physica D 84 (1995) 58-71.

トップに戻る

Submitted or In Preparation

• M.Nagayama, Y.Sanno, M.Denda, M.Tsutsumi, M.Goto, M.Nakatani, H.Kitahata and S.Nakata, " Mathematical model for a calcium wave induced by mechanical stimulus in keratinocytes " , in preparation.
• K.Nagai, K.Tachibana, Y.Tobe, H.Kitahata, M.Kazama, S.Omata and M.Nagayama, "Mathematical model for droplet motion with variational principle", in preparation.
• S.-I.Ei, M.Mimura and M.Nagayama, "Reflection of traveling spots ", in preparation.
• 矢留雅亮，上田肇一，長山雅晴，"反応拡散系に対する大域的分岐構造の数値計算法"，執筆中.

---

Proceedings, Reports, etc.

Proceedings

• 長山雅晴，安宅正，``樟脳船運動に現れる渋滞現象について”，計算工学講演会論文集，17(2012).
• 飯田渓太，北畑裕之，長山雅晴，``Numerical simulation of camphor motions at the air-water interface”，計算工学講演会論文集，17(2012).
• 長山雅晴，坂井昭彦，中田聡，北畑裕之，傳田光洋，``角層形成の数理モデル”，計算工学講演会論文集，16(2011).
• 長山雅晴，上田肇一，矢留雅亮，``反応拡散系に現れるカオスパルス波”，計算工学講演会論文集，15(2010).
• M.Mimura, M.Nagayama and T.Ohta, ``Non-annihilation of travelling pulses in reaction-diffusion system''，Proceedings of the International conference on Asyptotics in Nonlinear Diffusive Systems，Tohoku Math.Pub．8，239-245.

RIMS Kokyuroku (講究録)

• [紀１０]　長山雅晴，``現象の数理モデル，京都大学数理解析研究所講究録"，1768 (2011) 109-118.
• [紀９]　長山雅晴，坂井昭彦，傳田光洋，堤も絵，新妻真紀子，仲谷正史，中田聡，北畑裕之，``表皮細胞間カルシウムイオン波の伝播モデルについて”，京都大学数理解析研究所講究録, 1748 (2011) 141-155.
• [紀８]　長山雅晴，矢留雅亮，上田肇一，``Gray-Scottモデルと発熱反応拡散系に現れるパルス波ダイナミクス”，京都大学数理解析研究所講究録, 1680 (2010) 91-106.
• [紀７]　長山雅晴，参納由実，傳田光洋，堤も絵，新妻真紀子，中田聡，北畑裕之，``機械刺激による表皮細胞間カルシウム伝播の数理モデルについて”，京都大学数理解析研究所講究録, 1663 (2009) 206-211.
• ［紀６］　矢留雅亮，長山雅晴，上田肇一，``反応拡散系に対する大域的分岐構造の数値計算法とその応用''，京都大学数理解析研究所講究録，1633 (2009) 39-61．
• ［紀５］ T.Yamazaki, S.Omata and M.Nagayama, ``Numerical simulation of motion of a bubble restrained to water surface'', 京都大学数理解析研究所講究録, 1522 (2006) 111-119.
• ［紀４］ T.Ikeda, M.Nagayama and H.Ikeda, ``Bifurcation of helical wave from traveling wave'', 京都大学数理解析研究所講究録，1330 (2003) 40-55.
• ［紀３］ M.Nagayama, Y.Doi and S.Nakata, ``リン酸緩衝液上での樟脳酸運動の数理モデル''，京都大学数理解析研究所講究録，1313 (2003) 159-166.
• ［紀２］ T.IKeda and M.Nagayama, ``Numerical simulation of helical waves arising in self-propagating high-temperature syntheses'', 1191 (2001) 43-50.
• ［紀１］ M.Nagayama, T.Ikeda, T.Ishiwata and N.Tamura, ``反応拡散系に現れる螺旋進行波について'', 1167(2000) 13-24.

解説・著書

• ［解５］長山雅晴，現象の数理モデルをつくろう，数学セミナー，14--19，2012年8月号.
• ［解４］長山雅晴，角層形成の数理モデル，数学セミナー，14--18，2010年7月号.
• ［解３］長山雅晴, 樟脳運動の数理モデル, 数理科学, 12--17，2008年1月号.
• ［解２］長山雅晴，油滴運動の数理モデルとその数値計算法，物性研究，87(4)(2007)，617-619.
• ［解１］池田勉，長山雅晴，木村忠信，非平衡系の内部構造，数学セミナー，30-33，1996年6月号.
• ［書１］三村昌泰，長山雅晴，``パターン形成とダイナミクス（非線形・非平衡現象の数理４）第3章：発熱反応拡散系に現われる時空間パターン''，東京大学出版会，2006年2月．

予稿集他

2002年度以降更新を止めています.

• ショウノウ酸舟の数理モデル，日本応用数理学会 2001年度年会 講演予稿集，204-205
• 樟脳運動の数理モデルについて，日本応用数理学会 2000年度年会 講演予稿集，242-243
• 燃焼合成に現れる螺旋燃焼波の数値計算，日本応用数理学会 1999年度年会 講演予稿集，212-213
• 固形カンフェンの間欠運動について，応用数学合同研究集会報告集，167-168，2002
• リン酸緩衝液上での樟脳酸運動の数理モデル，応用数学合同研究集会報告集，183-184，2001年
• 表面張力を利用した樟脳運動の数理モデル，応用数学合同研究集会報告集，221-222，2000年
• 反応拡散系に現れる螺旋進行波について，応用数学合同研究集会報告集，215-216，1999年
• 燃焼合成反応モデルの数値計算，応用数学合同研究集会報告集，1998年
• Travelling Breatherのダイナミクスについて，応用数学合同研究集会報告集，281-284，1997年
• 単安定興奮系におけるパルスダイナミクスについて，応用数学合同研究集会報告集，329-332，1996年
• ある excitable system に現れるパターンダイナミクスについて，応用数学合同研究集会報告集，60-1-4，1995年
• 管状領域における発熱反応の断面形状依存性，応用数学合同研究集会報告集，50-1-6，1994年
• 燃焼過程におけるパターン形成，応用数学合同研究集会報告集，203-206，1993年

トップに戻る