TEL: 011-706-2891 ｜ 
Research Work
■研究紹介
表面張力を利用した物質運動の数理解析
・関連する研究費
・科学研究費補助金 若手研究（Ｂ），2002年度～2003年度
・科学研究費補助金 若手研究（Ａ），2006年度～2008年度
・科学研究費補助金 基盤研究（Ｂ），2009年度～2012年度
・科学研究費補助金 基盤研究（Ｂ），2016年度〜2019年度
・科学研究費補助金 基盤研究（Ｂ），2021年度〜2024年度
化学反応を伴う粒子運動の数理解析
液滴運動の数理モデルとその数理解析
液滴運動を表現する数理モデルは，液滴の高さを表現する変数を導入することによって，液滴の表面，水面を1つの関数を用いて表し，その関数を用いて表面エネルギー最小化から導出することに成功した．この方程式は特異性を持つ双曲型偏微分方程式となった．また，液滴から展開される界面活性膜を反応拡散系で近似することによって水面の表面張力変化を表現することにした．これと液滴の体積保存条件を加えることによって液滴運動を記述する数理モデルを構成した．この数理モデル中の液滴モデルが特異性を持つことと初期体積保存の制約条件を持つことから一般の差分による数値計算が困難であった．そこで離散勾配流を用いて数値計算をおこなった．その結果，１）小さな液滴は自走する，２）大きな液滴は分裂し自走する，３）分裂した液滴は衝突角度に依存して反射する場合と融合する場合がある，等の結果を得た．
液滴の融合現象
液滴の反射現象
ロウソク火炎振動子の同期現象に対する数理モデルとその数理解析
（科学研究費補助金 萌芽研究，2007年度～2009年度）
ロウソク火炎振動モデルの構成
複数の洋ロウソクを束ねて火をつけると炎が振動する現象がある． この炎が振動するロウソクの束をロウソク振動子と呼ぶことにする． ロウソク振動子を2つ用意して，適当に置くとロウソク振動子間の距離に 依存して炎の同期現象が報告された． この引き込み現象を起こす機構を数理的に理解することが研究の目的である． 1本のロウソクに火を点けると炎は一定形状を保ちながら燃焼し続けます．ところが，複数本束ねたロウソクに火を点けると炎の形状は一定周波数で振動しながら燃焼し続けるようになります．このロウソク火炎が振動する機構は，(ロウソクの本数が増えることで)ロウの供給と酸素の供給のバランスが崩れることによって生じる完全燃焼と不完全燃焼を繰り返すためだと考えられています． この振動している一組のロウソク火炎をロウソク振動子と呼ぶことにします． さて，このロウソク振動子を2組用意し並べて設置すると，その距離に応じて異なる同期現象が起こります．その距離が十分に近いと同位相同期し(図1(a))，適当に離れていると逆位相同期する(図1(b))ようになるのです． この同期現象はどのようにして起こっているのでしょうか？一見，2組のロウソクの酸素の奪い合いのように思えますが・・
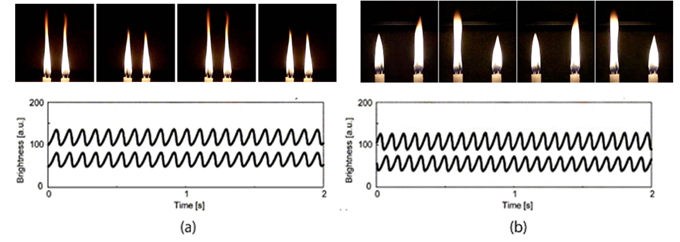
図1
工事中
生理学と協働した数理科学による皮膚疾患機構の解明
（ＪＳＴ CREST研究課題，2010年度～2015年度）
数理モデリングを基盤とした数理皮膚科学の創設
（ＪＳＴ CREST研究課題，2015年度～2020年度）
■Research Papers
[78] K. Xiong, M. Nagayama, K. Ijiro and H. Mitomo, Fair Surface Modification with Mixed Alkanethiols on Gold Nanoparticles through Minimal Unfair Ligand Exchange, to appear in Nanoscale Adv., 2024, DOI: 10.1039/D4NA00270A
[77] Y. Mai, Y. Kobayashi, H. Kitahata, T. Seo, T. Nohara, S. Itamoto, S. Mai, J. Kumamoto, M. Nagayama, W. Nishie, H. Ujiie, and K. Natsuga, Patterning in stratified epithelia depends on cell–cell adhesion, Life Science Alliance, 7 (9), e202402893 (18 July, 2024), DOI: 10.26508/lsa.202402893
[76] M. Yotsumoto, M. Matsuo, H. Kitahata, S. Nakanishi, M. Denda, M. Nagayama, and S. Nakata, Phospholipid Molecular Layer that Enhances Distinction of Odors Based on Artificial Sniffing, ACS Sensors, 8, 4494−4503(13 November 2023), https://doi.org/10.1021/acssensors.3c00382
[75] M. Nagayama*, H. Monobe, K. Sakakibara, K.-I. Nakamura, Y. Kobayashi, and H. Kitahata, On the reaction-diffusion type modelling of the self-propelled object motion, Scientific Reports, 13, 12633(25 July 2023), DOI: 10.1038/s41598-023-39395-w
[74] K. Imafuku, H. Iwata, K. Natsuga, M. Okumura, Y. Kobayashi, H. Kitahata, A. Kubo, M. Nagayama, H. Ujiie , Zonula occludens-1 distribution and barrier functions are affected by epithelial proliferation and turnover rates, Cell Proliferation, e13441, (14 March 2023), DOI: 10.1111/cpr.13441
[73] Y. Wang, H. Kitahata, H. Kosumi, M. Watanabe, Y. Fujimura, S. Takashima, S.-I. Osada, T. Hirose, W. Nishie, M. Nagayama, H. Shimizu and K. Natsuga*, Collagen XVII deficiency alters epidermal patterning, Laboratory Investigation, (10 February 2022), DOI:10.1038/s41374-022-00738-2
[72] Y. Yasugahira, M. Nagayama*, On a numerical bifurcation analysis of a particle reaction-diffusion model for a motion of two self-propelled disks, Japan J. Indust. Appl. Math. (17 January 2022), DOI: 10.1007/s13160-021-00498-4
[71] Y. Yasugahira, Y. Tatsumi, O. Yamanaka, H. Nishimori, M. Nagayama* and S. Nakata*, Catch and Release Chemotaxis, ChemSystemChem, , e202100031 (November 2021), DOI: 10.1002/syst.202100031
[70] K. Ohno, Y. Kobayashi, M. Uesaka, T. Gotoda, M. Denda, H. Kosumi, M. Watanabe, K. Natsuga, and M. Nagayama*, A Computational Model of the Epidermis With the Deformable Dermis and Its Application to Skin Diseases, Scientific Reports 11, 13234 (2021), DOI: 10.1038/s41598-021-92540-1
[69] M. Okamoto, T. Gotoda, and M. Nagayama*, Global existence of a unique solution and a bimodal travelling wave solution for the 1D particle-reaction-diffusion system, J. Phys. Commun. 5, 055016(2021), DOI: 10.1088/2399-6528/ac0100
[68] M. Nakatani*, Y. Kobayashi, K. Ohno, M. Uesaka, S. Mogami, Z. Zhao, T. Sushida, H. Kitahata, and M. Nagayama*, Temporal coherency of mechanical stimuli modulates tactile form perception, Scientific Reports 11, 11737 (2021), DOI: 10.1038/s41598-021-90661-1
[67] Y. Fujimura, M. Watanabe, K. Ohno, Y. Kobayashi, S. Takashima, H. Nakamura, H. Kosumi, Y. Wang, Y. Mai, A. Lauria, V. Proserpio, H. Ujiie, H. Iwata, W. Nishie, M. Nagayama, S. Oliviero, G. Donati, H. Shimizu, and K. Natsuga, Hair follicle stem cell progeny heal blisters while pausing skin development, EMBO Reports, e50882 (2021), DOI: 10.15252/embr.202050882
[66] M. Kim, M. Okamoto, Y. Yasugahira, S. Tanaka, S. Nakata, Y. Kobayashi, M. Nagayama*, A reaction-diffusion particle model for clustering of self-propelled oil droplets on a surfactant solution, Physica D, 425, 132949 (2021), DOI: 10.1016/j.physd.2021.132949
[65] J. Kumamoto, K. Fujimoto, Y. Kobayashi, K. Ohno, M. Nagayama and M. Denda, Substrate membrane bearing close-packed array of micron-level pillars incrassates air-exposed three-dimensional epidermal equivalent model, Skin Research and Technology, 27, 863-870 (2021), DOI: 10.1111/srt.13035
[64] M. Wang, X. Han, C. Liu, R. Takayama, T. Yasugi, S.-I. Ei, M. Nagayama, Y. Tanaka and M. Sato, Intracellular trafficking of Notch orchestrates temporal dynamics of Notch activity in the fly brain, Nature communications 12 (1), 1-15 (2021), DOI: 10.1038/s41467-021-22442-3
[63] M. Uesaka, K.-I. Nakamura, K. Ueda, and M. Nagayama, Stability of stationary points for one-dimensional Willmore energy with spatially heterogeneous term, Physica D 417, 132812(2021, March), DOI: 10.1016/j.physd.2020.132812
[62] S. Tanaka, S. Nakata, M. Nagayama, A surfactant reaction model for the reciprocating motion of a self-propelled droplet, Soft Matter 17, 388-396(2020, October), DOI: 10.1039/d0sm01500h
[61] J. Fan, M. Nagayama, G. Nakamuta, and M. Okamoto, A weak solution for a point mass camphor motion, Differential and Integral Equations 33(7-8), 431-443(2020, August).
[60] M. Okamoto, T. Gotoda and M. Nagayama*, Existence and non‑existence of asymmetrically rotating solutions to a mathematical model of self-propelled motion, Japan J. Indust. Appl. Math. 37(3), 883-912 (2020, June), DOI: 10.1007/s13160-020-00427-x
[59] Y. Hirose, Y. Yasugahira, M. Okamoto, Y. Koyano, H. Kitahata, M. Nagayama, and Y. Sumino, Two floating camphor particles interacting through the lateral capillary force, J. Phys. Soc. Jpn. 89(7), 074004(2020, May), DOI: 10.7566/JPSJ.89.074004
[58] S. Ipponjima, Y. Umino, M. Nagayama, M. Denda, Live imaging of alterations in cellular morphology and organelles during cornification using an epidermal equivalent model, Scientific Reports 10, 5515(2020, March), DOI: 10.1038/s41598-020-62240-3
[57] K. Ikeda, S-.I. Ei, M.Nagayama, M. Okamoto, and A. Tomoeda, Reduced model of a reaction-diffusion system for the collective motion of camphor boats, Physical Review E 99, 062208(2019, June), DOI: 10.1103/PhysRevE.99.062208
[56] J. Kumamoto, S. Nakanishi, M. Kakita, M. Uesaka, Y. Yasugahira, Y. Kobayashi, M. Nagayama, S. Denda, and M. Denda, Mathematical-model-guided development of full-thickness epidermal equivalent, Scientific Reports 8, 17999(2018, December), DOI: https://doi.org/10.1038/s41598-018-36647-y
[55] Y. Kobayashi, Y. Yasugahira, H. Kitahata, M. Watanabe, K. Natsuga and M. Nagayama*, Interplay between epidermal stem cell dynamics and dermal deformation, npj Computational Materials 4(1), 45 (2018, August), DOI: 10.1038/s41524-018-0101-z
[54] Y. Tanaka, T Yasugi, M. Nagayama M. Sato and S. -I. Ei, JAK/STAT guarantees robust neural stem cell differentiation by shutting off biological noise, Scientific Reports 8, 12484 (2018, August), DOI: 10.1038/s41598-018-30929-1
[53] S. Nakata, K. Kayahara, M. Kuze, E. Ginder, M. Nagayama and H. Nishimori, Synchronization of self-propelled soft pendulums, Soft Matter 14, 3791-3798(2018, Apr.), DOI: 10.1039/C8SM00517F
[52] T. Shinoda, A. Nagasaka, Y. Inoue, R. Higuchi, Y. Minami, K. Kato, M. Suzuki, T. Kondo, T. Kawaue, K. Saito, N. Ueno, Y. Fukazawa, M. Nagayama, T. Miura, T. Adachi, and T. Miyata, Elasticity-based boosting of neuroepithelial nucleokinesis via indirect energy transfer from mother to daughter, PLoS Biol. 16(4), e2004426(2018, Apr.), DOI: 10.1371/journal.pbio.2004426
[51] S.-I. Ei, H Kitahata, Y. Koyano, and M. Nagayama, Interaction of non-radially symmetric camphor particles, Physica D 368(1), 10-26(2018), DOI: 10.1016/j.physd.2017.11.004
[50] E. Ginder, T. Minomo, M. Nagayama, S. Nakata and H. Yamamoto, Traveling pulse solutions in a point mass model of diffusing particles, Computer Methods in Materials Science 17(2), 111-121(2017)
[49] Y. Kobayashi, H. Kitahata, and M. Nagayama, Sustained dynamics of a locally excitable system with nonlocal interactions, Physical Review E 96,022213(2017), DOI: 10.1103/PhysRevE.96.022213
[48] M. Watanabe, K. Natsuga, W. Nishie, Y. Kobayashi, G. Donati, S. Suzuki, Y. Fujimura, T. Tsukiyama, H. Ujiie, S. Shinkuma, H. Nakamura, M. Murakami, M. Ozaki, M. Nagayama, F. M Watt, H. Shimizu, Type XVII collagen coordinates proliferation in the interfollicular epidermis, eLife 6, e26635(2017), DOI: 10.7554/eLife.26635
[47] Y. Satoh, Y. Sogabe. K. Kayahara, S. Tanaka, M. Nagayama and S. Nakata, Self-inverted reciprocation of an oil droplet on a surfactant solution, Soft Matter 13, 3422-3430(2017), DOI: 10.1039/c7sm00252a.
[46] J. Kumamoto, M. Goto, M. Nagayama and M. Denda, Real-time imaging of human epidermal calcium dynamics in response to point laser stimulation, Journal of Dermatological Science 86(1):13-20(2017), DOI: 10.1016/j.jdermsci.2017.01.002.
[45] M. Sato, T. Yasugi, Y. Minami, T. Miura, and M. Nagayama, Notch-mediated lateral inhibition regulates proneural wave propagation when combined with EGF-mediated reaction diffusion, PNAS 113, 35(2016), DOI: 10.1073/pnas.1602739113.
[44] K. Nagai, K. Tachibana, Y. Tobe, M. Kazama, H. Kitahata, S. Omata and M. Nagayama, Mathematical model for self-propelled droplets driven by interfacial tension, Journal of Chemical Physics 144, 114707 (2016), DOI: 10.1063/1.4943582.
[43] Y. Kobayashi, Y. Sawabu, H. Kitahata, M. Denda, M. Nagayama, Mathematical model for calcium-assisted epidermal homeostasis, Journal of Theoretical Biology 397(2016), 52–60, DOI: 10.1016/j.jtbi.2016.02.032.
[42] K. Takei, S. Denda, M. Nagayama, M. Denda, Role of STIM1-Orai1 system in intracellular calcium elevation induced by ATP in cultured human keratinocytes, Exp Dermatol. 25(4), 323-325 (2016), DOI: 10.1111/exd.12928
[41] J. Kumamoto, M. Tsutsumi, M. Goto, M. Nagayama and M. Denda, Japanese Cedar (Cryptomeria japonica) pollen allergen induces elevation of intracellular calcium in human keratinocytes and impairs epidermal barrier function of human skin ex vivo, Arch Dermatol Res 308(1), 49-54(2015), DOI: 10.1007/s00403-015-1602-y
[40] Y. Kobayashi, H. Kitahata, and M. Nagayama, Model for calcium-mediated reduction of structural fluctuations in epidermis, Physical Review E 92(2015), 022709, DOI: 10.1103/PhysRevE.92.022709
[39] T. Mori, K. Kuto, M. Nagayama, T. Tsujikawa, S. Yotsutani, Global bifurcation sheet and diagrams of wave-pinning in a reaction-diffusion model for cell polarization, Dynamical Systems, Differential Equations and Applications AIMS Proceedings, 861- 877(2015), DOI:10.3934/proc.2015.0861
[38] J. Kumamoto, H. Kitahata, M. Goto, M. Nagayama and M. Denda, Effects of medium flow on axon growth with or without nerve growth factor, Biochemical and Biophysical Research Communications 465(1), 26-29(2015), DOI:10.1016/j.bbrc.2015.07.104.
[37] K. Nishi, T. Ueda, M. Yoshii, Y. S. Ikura, H. Nishimori, S. Nakata and M. Nagayama, Bifurcation phenomena of two self-propelled camphor disks on an annular field depending on system length, Phys.Rev.E 92(2015), 022910, DOI: 10.1103/PhysRevE.92.022910
[36] M. Tsutsumi, H. Kitahata, M. Fukuda, J. Kumamoto, M. Goto, S. Denda, K. Yamasaki, S. Aiba, M. Nagayama and M. Denda, Numerical and comparative three-dimensional structural analysis of peripheral nerve fibers in epidermis of atopic dermatitis patients, British Journal of Dermatology 174(1), 191-194(2016), DOI: 10.1111/bjd.13974.
[35] M. Tsutsumi, M. Fukuda, J. Kumamoto, M. Goto, S. Denda, K. Yamasaki, S. Aiba, M. Nagayama and M. Denda, Abnormal Morphology of Blood Vessels in Erythematous Skin From Atopic Dermatitis Patients, The American Journal of dermatopathology 465(1), 26-29(2015), DOI: 10.1097/DAD.0000000000000373.
[34] S.-I. Ei, K. Ikeda, M. Nagayama and A. Tomoeda, Reduced model from a reaction-diffusion system of collective motion of camphor boats, Discrete and Continuous Dynamical Systems Series-S 8(5), 847-856(2015), DOI: 10.3934/dcdss.2015.8.847.
[33] S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu, and T. Hasegawa, Physicochemical design and analysis of self-propelled objects that are characteristically sensitive to interfacial environments, Physical Chemistry Chemical Physics 7, 10326-10338(2015), DOI: 10.1039/C5CP00541H.
[32] S.-I. Ei, K. Ikeda, M. Nagayama and A. Tomoeda, Application of a center manifold theory to a reaction-diffusion system of collective motion of camphor disks and boats, Mathematica Bohemica 139(2), 363-371(2014).
[31] Y. Kobayashi, Y. Sanno, A. Sakai, Y. Sawabu, M. Tsutsumi, M. Goto, H. Kitahata, S. Nakata, J. Kumamoto, M. Denda, M. Nagayama, Mathematical modeling of calcium waves induced by mechanical stimulation in keratinocytes, PLoS ONE 9(3), e92650(2014), DOI: 10.1371/journal.pone.0092650
[30] K. Iida, H. Kitahata and M. Nagayama, Theoretical study on the translation and rotation of an elliptic camphor particle, Physica D 272(2014), 39-50, DOI: 10.1016/j.physd.2014.01.005.
[29] M. Denda, S. Denda, M. Tsutsumi, M. Goto, J. Kumamoto, M. Nakatani, K. Takei, H. Kitahata, S. Nakata, Y. Sawabu, Y. Kobayashi, M. Nagayama, Frontiers in epidermal barrier homeostasis – an approach to mathematical modeling of epidermal calcium dynamics, Experimental Dermatology 23(2014), 79-82, DOI: 10.1111/exd.12302
[28] S. Nakata, T. Miyaji T. Ueda, T. Sato, Y. S. Ikura, S. Izumi and M. Nagayama, Reciprocating motion of a self-propelled object on a molecular layer with a local minimum and a local maximum isotherm, Journal of Physical Chemistry C 117(2013) 6346-6352, DOI: 10.1021/jp400971h
[27] T. Hirashima, Y. Hosokawa, T. Iino, and M. Nagayama, On Fundamental Cellular Processes for Emergence of Collective Epithelial Movement, Biology Open 2(7)2013, 660-666, DOI: 10.1242/bio.20134523
[26] H. Kitahata, K. Iida and M. Nagayama, Spontaneous motion of an elliptic camphor particle, Physical Review E 87(2013)010901, DOI:10.1103/PhysRevE.83.056207
[25] M. Yadome, K-I. Ueda and M. Nagayama, Chaotic motion of propagating pulses in the Gray-Scott model, Physical Review E 83(2011) 056207, DOI: 10.1103/PhysRevE.83.056207
[24] M. Nagayama, K-I. Ueda and M. Yadome, Numerical approach for transient dynamics of oscillatory pulses in a bistable reaction-diffusion system, Japan Journal of Industrial and Applied Mathematics, 27(2) (2010) 295-322, DOI: 10.1007/s13160-010-0015-8
[23] N. J. Suematsu, Y. Ikura, M. Nagayama, N. Kawagishi, M. Nakamura, H. Kitahata, M. Murakami and S. Nakata, Mode-switching of the self-motion of a camphor boat depending on the diffusion distance of camphor molecules, Journal of Physical Chemistry, 114(2010) 9876-9882, DOI: 10.1021/jp101838h.
[22] K. Iida, N. J. Suematsu, Y. Miyahara, H. Kitahata, M. Nagayama and S. Nakata, Experimental and theoretical studies on the self-motion of a phenanthroline disk coupled with complex formation, Physical Chemistry Chemical Physics, 12(2010) 1557-1563, DOI: 10.1039/B918691C.
[21] M. Tsutsumi, H. Kitahata, S. Nakata, Y. Sanno, M. Nagayama and M. Denda, Mathematical analysis of intercellular calcium propagation induced by adenosine triphosphate, Skin Research and Technology, 16(2010) 146-150, DOI: 10.1111/j.1600-0846.2009.00420.x.
[20] H. Kitahata, J. Taguchi, M. Nagayama, T. Sakurai, Y. Ikura, A. Osa, Y. Sumino, M. Tanaka, E. Yokoyama and H. Miike, Oscillation and synchronization in combustion of candles: Radiation coupling could induce synchronization of oscillatory combustion, Journal of Physical Chemistry (A), 113(29) (2009) 8164-8168.
[19] M. Nagayama, M. Yadome, N. Kato, J. Kirisaka, M. Murakami and S. Nakata, Bifurcation of self-motion depending on the reaction order, Physical Chemistry Chemical Physics, 11(2009) 1085-1090.
[18] M. Yadome, K.-I. Ueda, T. Teramoto, M. Nagayama and Y. Nishiura, A nested sequence of transitions for collision dynamics in dissipative systems, Bulletin of the Institute of Mathematics, Academia Sinica New Series, 3(4)(2008) 585-601.
[17] S.-I. Ei, M. Mimura and M. Nagayama, Interacting spots in reaction diffusion systems, Discrete and Continuous Dynamical Systems, 14(1)(2006) 31-62.
[16] Y. Sumino, M. Nagayama, H. Kitahata, S. M. Nomura, N. Magome, Y. Mori and K. Yoshikawa, Chemo-Sensitive Running Droplet, Physical Review E 72(2005) 041603.
[15] T. Ikeda, M. Nagayama and H. Ikeda, Bifurcation of helical wave from travelling wave, Jpn. J. Indast. Appl. Math. 21(3)(2004) 405-424.
[14] M. Nagayama, S. Nakata, Y. Doi, and Y. Hayashima, A theoretical and experimental study on the unidirectional motion of a camphor disk, Physica D, 194(2004) 151-165.
[13] M. Mimura, M. Nagayama and T. Ohta, Non-annihilation of travelling pulses in reaction-diffusion systems, Methods and Applications of Analysis, 9(4)(2002) 493-516.
[12] S.-I. Ei, M. Mimura and M. Nagayama, Pulse-pulse interaction in Reaction-Diffusion system, Physica D, 165(2002) 176-198.
[11] Y. Hayashima, M. Nagayama, Y. Doi, S. Nakata, M. Kimura, and M. Iida, Self-motion of a camphoric acid boat sensitive to chemical environment, Phys.Chem.Chem.Phys.,4(2002) 1386-1392. DOI: 10.1039/B108686C
[10] M. Nagayama, H. Okamoto and J. Zhu, On the blow-up of some similarity solutions of the Navier-Stokes equations, Quaderni di Matematica 10 (2002) 139-162.
[9] M. Nagayama and H. Okamoto, On the interior layer appearing in the similarity solutions of the Navier-Stokes equations, Jpn. J. Indast. Appl. Math. 19(2) (2002) 277-300.
[8] M. Nagayama, T. Ikeda, T.Ishiwata, N. Tamura and M. Ohyanagi, Three-dimensional numerical simulation of helically propagating combustion waves, Journal of Materials Synthesis and Processing 9(3) (2001) 153-163.
[7] M. I. Kohira, Y. Hayashima, M. Nagayama, and S. Nakata, Synchronized self-motion of two camphor boats, Langmuir 17 (22)(2001) 7124-7129. DOI: 10.1021/la010388r
[6] T. Ikeda and M. Nagayama, Helical Combustion Waves in Self-propagating High-temperature Syntheses, Bulletin of the Japan Society for Industrial and Applied Mathematics 11(2) (2001) 40-48 (in Japanese). DOI: 10.11540/bjsiam.11.2_132
[5] Y. Hayashima, M. Nagayama, and S. Nakata, A camphor grain oscillates while breaking symmetry, Journal of Physical Chemistry B 105(22) (2001) 5353-5357. DOI: 10.1021/jp004505n
[4] M. Mimura, M. Nagayama, H. Ikeda and T. Ikeda, Dynamics of travelling breathers arising in reaction-diffusion systems – ODE modelling approach –, Hiroshima Math. J. 30(2) (2000) 221-256.
[3] M. Mimura, M. Nagayama and K. Sakamoto, Singular Hopf-bifurcation in a chemical reaction-diffusion system, Appl. Math. Lett. 11(4) (1998) 127-131.
[2] M. Mimura and M. Nagayama, Nonannihilation dynamics in an exothermic reaction-diffusion system with mono-stable excitability, CHAOS 7(4) (1997) 817-826.DOI: 10.1063/1.166282
[1] M. Mimura, M. Nagayama and K. Sakamoto, Pattern dynamics in an exothermic reaction, Physica D 84 (1995) 58-71.
● Submitted Papers
■ Proceedings, Reports, etc.
● Proceedings
[p28] Eom Junyong，内海晋弥，上田祐暉，Gao Yueyuan，中岡 慎治，水藤 寛，久米 真司，片桐 秀樹，長山 雅晴，”Parameter estimation and analysis of 9-compartment mathematical model for glucose-insulin dynamics”, 計算工学講演会論文集，29 (2024)．
[p27] 香川渓一郎，奥村真善美，小林康明，Duligengaowa Wuergezhen，森田梨津子，藤原裕展，長山雅晴，”線維芽細胞に注目した毛包形態形成の数理モデル”，計算工学講演会論文集，29 (2024)．
[p26] 奥村真善美，長山雅晴，小林康明，後藤真紀子，宮井雅史，中西忍，菅原美郷，”ある細胞接着タンパクの分解酵素を考慮した角層剥離モデル”，計算工学講演会論文集，28 (2023)．
[p25] 奥村真善美，小林康明，長山雅晴，藤原裕展，安ヶ平裕介，大野航太，”塑性変形可能な基底膜モデルを用いた毛包形成メカニズムの数理的考察”、計算工学講演会論文集, 27，456-459 (2022).
[p24] 長山雅晴、”数理科学と医学・生命科学との連携 〜皮膚科学との連携を例にして”，医学の歩み，279(3), 217–222 (2021)
[p23] 小林康明， 大野航太， 長山雅晴，”真皮の塑性変形と形態形成の数理モデル構築”，計算工学講演会論文集, 26 (2021)
[p22] 大野航太， 小林康明，熊本淳一，傳田光洋，長山雅晴，”表皮構造の数理モデルにおける基底膜形状と培養皮膚への応用”，計算工学講演会論文集, 26 (2021)
[P21] 大野航太， 小林康明， 後藤田剛， 上坂正晃， 安ケ平祐介， 北畑裕之， 傳田光洋， 長山雅晴，”表皮構造の数理モデルを用いた皮膚疾患への応用”，計算工学講演会論文集，25（2020）
[P20] 上坂 正晃，後藤田 剛，一本嶋 佐理，北畑 裕之，小林 康明，安ヶ平 裕介，傳田 光洋，長山 雅晴，”表皮構造の数理モデルにおける細胞の扁平化と細胞の多面体形状について”，計算工学講演会論文集，24（2019）
[P19] 後藤田剛，上坂正晃，安ヶ平祐介，小林康明，北畑裕之，傳田光洋，長山雅晴，”表皮数理モデルにおける皮膚バリア機能の恒常性”，計算工学講演会論文集，24(2019)
[P18] 後藤田剛，上坂正晃，安ヶ平祐介，小林康明，北畑裕之，傳田光洋，長山雅晴，”表皮における顆粒層の安定性とタイトジャンクション形成の数理モデリング”，計算工学講演会論文集，23(2018)
[P17] 長山雅晴，小林康明，安ヶ平裕介，熊本淳一，傳田光洋，北畑裕之，中田聡，”皮膚疾患再現を目指した皮膚構造数理モデル”，計算工学講演会論文集，22(2017)
[P16] 田中吉太郎，八杉徹雄，佐藤純，長山雅晴，栄伸一郎，”分化の波のノイズ抑制機構に対する数理モデリングと実験からのアプローチ”，計算工学講演会論文集，22(2017)
[P15] 長山雅晴，小林康明，傳田光洋，北畑裕之，”角層バリア機能の数理モデルとその応用”，応用数理，27(2), 18-26(2017), https://doi.org/10.11540/bjsiam.27.2_18（査読付き）
[P14] 長山雅晴，小林康明，熊本淳一，傳田光洋，北畑裕之，中田聡，”真皮形状を伴う表皮構造の数理モデリング”，計算工学講演会論文集，21(2016)
[P13] 小林康明，北畑裕之，長山雅晴，”表皮の連続体モデルによる真皮形状と角層形状についての解析”，計算工学講演会論文集，20(2015)
[P12] 長山雅晴，小林康明，澤武裕輔，久保実沙貴，傳田光洋，北畑裕之，中田聡，”真皮形状を考慮した皮膚構造の数理モデリング”，計算工学講演会論文集，20(2015)
[P11] 長山雅晴，小林康明，熊本淳一，澤武裕輔，傳田光洋，中田聡，北畑裕之，”表皮構造の数理モデリング”，マス・フォア・インダストリー研究，3(2015)17-25.
[P10] Y. Kobayashi, Y. Sawabu, S. Ota and M. Nagayama, Mathematical model for epidermal homeostasis, Mathematical Progress in Expressive Image Synthesis II: Proceedings of the Symposium 2014, Mathematics for Industry 18( H. Ochiai, K. Anjyo Eds.) , 119-124(2015), Springer.（査読付き）
[P09] Y. Kobayashi and M. Nagayama, Mathematical model of epidermal structure, Applications + Practical Conceptualization + Mathematics = fruitful Innovation: Proceedings of the Forum of Mathematics for Industry 2014, Mathematics for Industry 11(R.S. Anderssen et al. Eds.), 121-126(2015), Springer.（査読付き）
[P08] 長山雅晴，若井健，小林康明，西慧，井倉 S. 弓彦，中田聡，”樟脳円盤の集団運動に対する計算機援用解析”，計算工学講演会論文集，19(2014).
[P07] 長山雅晴，小林康明，澤武裕輔，中田聡，北畑裕之，後藤真紀子，堤も絵，傳田光洋，”表皮構造の数理モデル”，計算工学講演会論文集，18(2013).
[P06] 飯田渓太，北畑裕之，長山雅晴，”樟脳粒の自発運動：粒子形状と運動の関係について”，計算工学講演会論文集，18(2013).
[P05] 長山雅晴，安宅正，”樟脳船運動に現れる渋滞現象について”，計算工学講演会論文集，17(2012).
[P04] 飯田渓太，北畑裕之，長山雅晴，Numerical simulation of camphor motions at the air-water interface，計算工学講演会論文集，17(2012).
[P03] 長山雅晴，坂井昭彦，中田聡，北畑裕之，傳田光洋，”角層形成の数理モデル”，計算工学講演会論文集，16(2011).
[P02] 長山雅晴，上田肇一，矢留雅亮，”反応拡散系に現れるカオスパルス波”，計算工学講演会論文集，15(2010).
[P01] M.Mimura, M.Nagayama and T.Ohta, Non-annihilation of travelling pulses in reaction-diffusion system，Proceedings of the International Conference on Asymptotics in Nonlinear Diffusive Systems，Tohoku Math.Pub．8，239-245.
●RIMS Kokyuroku (講究録)
[紀１１] 長山雅晴，小林康明，澤武祐輔，久保実沙貴，傳田光洋，中田聡，北畑裕之，”表皮構造の数理モデル，京都大学数理解析研究所講究録”，1957(2015)155ｰ168．
[紀１０] 長山雅晴，”現象の数理モデル”，京都大学数理解析研究所講究録”，1768 (2011) 109-118.
[紀９] 長山雅晴，坂井昭彦，傳田光洋，堤も絵，新妻真紀子，仲谷正史，中田聡，北畑裕之，”表皮細胞間カルシウムイオン波の伝播モデルについて”，京都大学数理解析研究所講究録, 1748 (2011) 141-155.
[紀８] 長山雅晴，矢留雅亮，上田肇一，”Gray-Scottモデルと発熱反応拡散系に現れるパルス波ダイナミクス”，京都大学数理解析研究所講究録, 1680 (2010) 91-106.
[紀７] 長山雅晴，参納由実，傳田光洋，堤も絵，新妻真紀子，中田聡，北畑裕之，”機械刺激による表皮細胞間カルシウム伝播の数理モデルについて”，京都大学数理解析研究所講究録, 1663 (2009) 206-211.
[紀６] 矢留雅亮，長山雅晴，上田肇一，”反応拡散系に対する大域的分岐構造の数値計算法とその応用”，京都大学数理解析研究所講究録，1633 (2009) 39-61．
[紀 ５] T.Yamazaki, S.Omata and M.Nagayama, “Numerical simulation of motion of a bubble restrained to water surface”, 京都大学数理解析研究所講究録, 1522 (2006) 111-119.
[紀４] T.Ikeda, M.Nagayama and H.Ikeda, “Bifurcation of helical wave from traveling wave”, 京都大学数理解析研究所講究録，1330 (2003) 40-55.
[紀３] M.Nagayama, Y.Doi and S.Nakata, “リン酸緩衝液上での樟脳酸運動の数理モデル”，京都大学数理解析研究所講究録，1313 (2003) 159-166.
[紀 ２] T.IKeda and M.Nagayama, “Numerical simulation of helical waves arising in self-propagating high-temperature syntheses”, 1191 (2001) 43-50.
[紀１] M.Nagayama, T.Ikeda, T.Ishiwata and N.Tamura, “反応拡散系に現れる螺旋進行波について”, 1167(2000) 13-24.
●解説・著書
[解9] 長山雅晴，Coffee Break「つながるゆく縁に感謝」，数学セミナー，1，2022年1月号．
[解8] 長山雅晴，Coffee Break「私の夢」，数学セミナー，1，2021年7月号．
[解７] 長山雅晴，現象の数理モデリング〜化学反応モデルを中心に〜，数学通信，23(4), 2018.
[著3] Satoshi Nakata, Masaharu Nagayama, Theoretical and Experimental Design of Self-propelled Objects Based on Nonlinearity, Self-organized Motion, 1-30, 2018.
[著2] Hiroyuki Kitahata, Yuki Koyano, Keita Iida, Masaharu Nagayama, Mathematical Model and Analyses on Spontaneous Motion of Camphor Particle, Self-organized Motion, 31-62, 2018.
[解６] 長山雅晴，樟脳船の数理モデル，数学セミナー，8–12，2015年2月号．
[解５] 長山雅晴，現象の数理モデルをつくろう，数学セミナー，14–19，2012年8月号.
[解４] 長山雅晴，角層形成の数理モデル，数学セミナー，14–18，2010年7月号.
[解３] 長山雅晴, 樟脳運動の数理モデル, 数理科学, 12–17，2008年1月号.
[解２] 長山雅晴，油滴運動の数理モデルとその数値計算法，物性研究，87(4)(2007)，617-619.
[解１] 池田勉，長山雅晴，木村忠信，非平衡系の内部構造，数学セミナー，30-33，1996年6月号.
[書 １] 三村昌泰，長山雅晴，パターン形成とダイナミクス（非線形・非平衡現象の数理４）第3章：発熱反応拡散系に現われる時空間パターン，東京大学出版 会，2006年2月．
